Artículos
Estimación del exceso de mortalidad asociada a la pandemia COVID-19 para la Ciudad de Buenos Aires. Años 2020 y 2021
Estimación del exceso de mortalidad asociada a la pandemia COVID-19 para la Ciudad de Buenos Aires. Años 2020 y 2021
Población de Buenos Aires, vol. 20, núm. 32, 2023
Gobierno de la Ciudad de Buenos Aires

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional.
Recepción: 28 Agosto 2023
Aprobación: 23 Octubre 2023
Resumen: Ahora que se dispone de las estadísticas vitales completas hasta el año calendario 2021 inclusive, la propuesta del presente trabajo consiste en utilizar la serie de defunciones ocurridas y registradas en la Ciudad de Buenos Aires durante el período 2014-2019, para estimar, por medio de la aplicación de diversas técnicas estadísticas, las defunciones esperadas en el bienio 2020-2021, en un escenario de no pandemia. En tal sentido, se pretende replicar, para la Ciudad de Buenos Aires los resultados, de los conceptos y métodos incorporados en una publicación de la Organización Mundial de la Salud que promueve la realización de estos cálculos. Las diferencias entre las defunciones estimadas y aquellas efectivamente observadas, en caso de ser significativas, serían atribuibles a COVID-19. Esto no necesariamente significa que las diferencias respecto de lo esperado hayan sido producto de defunciones ocurridas por esa causa, pero sí a causa de la pandemia y todo el conjunto de acontecimientos que derivó de la pandemia y de la cuarentena.
Palabras clave: COVID-19, exceso, modelo, mortalidad, pandemia.
Abstract: Now that vital statistics are available and up-to-date to the calendar year 2021, the aim of this article is to use the time-series of deaths occurred and registered in the City of Buenos Aires during the period 2014-2019 to estimate, through diverse statistical techniques, the expected deaths for 2020 and 2021. The main idea is to replicate –for the City of Buenos Aires– the concepts and methods introduced in an article published by the World Health Organization in which these calculations are encouraged and promoted. The significant differences between the observed deaths and those expected under regular trends would eventually be attributed to COVID-19. This does not necessarily mean that those deaths are caused directly by the virus, but instead that they are deaths somehow related to it: they might have also been caused by the pandemics itself, the quarantine experienced and the new reality experienced those years.
Keywords: COVID-19, excess, model, mortality, pandemics.
Introducción
En diciembre de 2019, nadie esperaba lo que el mundo habría de vivir en los años inmediatamente próximos. La pandemia COVID-19 ha sido mucho más mortal que la gripe española de 1918 y que otras pandemias que se han sucedido a lo largo de la historia (Cavaillon y Osuchowsky, 2021; Lachenal y Thomas, 2020; Pitlik, 2020). Por otra parte, como es sabido, los efectos de la pandemia COVID-19 se han expandido alrededor de todo el mundo, tanto en su dimensión sanitaria como social y económica. Junto con la aparición de un virus nuevo y desconocido, las autoridades sanitarias y gubernamentales de todo el mundo han implantado una serie de medidas novedosas para paliar el efecto contagio de este virus, entre ellas los confinamientos y cuarentenas.
Este nuevo escenario, se supone, resultó en un aumento de muertes por la aparición de un nuevo virus letal, en un aumento de muertes por otras causas que no pudieron ser atendidas en tiempo y forma, pero también, en una disminución de muertes por otras causas que se lograron evitar como, por ejemplo, los accidentes de tránsito que se redujeron por las prohibiciones de circular.
A lo largo de toda la pandemia, la Organización Mundial de la Salud ha estado monitoreando el impacto a través de la difusión, en su portal, de estadísticas diversas tales como número de casos, número de defunciones, número de vacunados. Este portal se ha ido actualizando en la medida en que los datos de diferentes territorios estuvieron disponibles. Sin embargo, la misma organización consideró que esta información resultaba insuficiente para tener una imagen completa del impacto de la pandemia, por lo que, en abril de 2023, se publicó “Methods for estimating the excess mortality associated with the COVID-19 pandemic”, un ensayo que había sido publicado anteriormente, pero fue sometido a sucesivas revisiones y versiones mejoradas. Esta publicación tuvo como objetivo proponer diferentes metodologías para medir el impacto de la pandemia en la mortalidad, proveyendo técnicas y procesamientos para distintos territorios con distintas realidades en cuanto a la captación de datos y a su calidad. Las técnicas estadísticas que el documento presenta –y que en este trabajo se replican– ya habían sido utilizadas también por distintos autores para estimaciones relacionadas con la pandemia (Djakaria y Saleh, 2021; Guleryuz, 2021; Jain et al., 2021, Nikparvar et al., 2021, Perone, 2022; Safi y Sanusi, 2021).
En este artículo, la propuesta es tomar como punto de partida la publicación mencionada de la Organización Mundial de la Salud, que a lo largo del texto se irá detallando, y realizar el ejercicio propuesto de medir lo que se da en llamar “exceso de mortalidad” (o “defecto de mortalidad”) asociado a la pandemia, en la Ciudad de Buenos Aires. La idea general no tiene que ver con contabilizar muertes directamente atribuibles al virus, sino con comparar las defunciones observadas con aquellas que se hubieran esperado en un escenario sin pandemia. Se supone que, de no haber errores de cobertura o de cabalidad, las diferencias son atribuibles tanto al virus en sí como a todo el conjunto de medidas y de realidades que acompañaron el cambio de vida que todo el planeta experimentó en 2020 y en 2021. En el documento base existe una estimación efectuada, pero para Argentina y, por otra parte, fue hecha cuando no se contaba con la información de las estadísticas vitales con la que se cuenta hoy, por lo que fue necesario realizar múltiples ajustes para estimar la información faltante (Karlinsky, 2022). En este trabajo, el objetivo principal es explorar las técnicas indicadas en aquel documento y replicarlas. Se trata de técnicas esencialmente econométricas, por lo que el presente artículo tiene un enfoque predominantemente estadístico, a diferencia de otros estudios que presentan un enfoque epidemiológico o demográfico.
A los fines del presente artículo y con la información proveniente del sistema de estadísticas vitales de la Ciudad, en conjunto con la aplicación de las diversas técnicas estadísticas propulsadas por el documento base, se procederá a cuantificar y traducir a indicadores este nuevo escenario descripto. Para llevar adelante este objetivo, en una primera sección se identificará y describirá la fuente de datos a utilizar, sus ventajas y sus limitaciones, para luego pasar a describir las técnicas que se emplearán, sus supuestos y consideraciones de tipo metodológicas. Hechas las aclaraciones respecto de la fuente y la metodología, se describirá en forma sucinta la evolución de la mortalidad durante los seis años calendarios precedentes a la pandemia, 2014 a 2019 inclusive, y los patrones que resulten de este análisis serán considerados los “habituales” a los fines de este trabajo. A pesar de que el documento base sugiere tomar los cinco años anteriores a la pandemia, se ha decidido incorporar la información del año 2014, puesto que alrededor del año 2015, como se verá más adelante, el número total de defunciones de la Ciudad ha fluctuado y no presenta un comportamiento monótono. En la posterior sección, se elaboran proyecciones de la mortalidad esperada para los años 2020 y 2021, bajo estas condiciones habituales, para después ser comparadas en forma directa con el efectivo de muertes observado en el territorio de análisis; es decir, la Ciudad de Buenos Aires. Finalmente, se resumirán las conclusiones del trabajo y se invitará a continuar abordando la temática desde distintas perspectivas, a modo de lineamientos futuros.
Fuentes de datos
Como es sabido, en Argentina existe un sistema de estadísticas vitales basado en el registro civil, entidad cuya finalidad jurídica es la registración legal de los hechos vitales (nacimientos, defunciones, matrimonios, divorcios, adopciones, entre otros). Siguiendo a Naciones Unidas (2003), el registro civil supone “la anotación continua, permanente, obligatoria y universal de los hechos ocurridos y sus características, en particular, los hechos concernientes al estado civil de las personas, dispuesta por decreto o reglamentación, según las disposiciones legales de cada país” (p. 7). Los documentos (actas) derivados de esta registración constituyen instrumentos legales que permiten a las personas o a sus familiares probar diversos hechos, como pueden ser la edad, el estado civil o la muerte, los cuales generan derechos u obligaciones. Paralelamente, cumple un objetivo estadístico porque cada hecho civil supone, además, completar un informe estadístico. De esta manera, un sistema de estadísticas vitales se define como el proceso total consistente en a) recoger información, mediante el registro civil o empadronamiento, sobre la frecuencia de determinados sucesos vitales, así como sobre las características pertinentes de los propios hechos y de la persona o personas a que estos se refieren, y b) recopilar, procesar, analizar, evaluar, presentar y difundir esos datos en forma estadística (Naciones Unidas, 2003). En el sistema de estadísticas vitales de Argentina, el Ministerio de Salud de la Nación es la autoridad responsable del cómputo, consistencia y publicación final de los registros de defunciones. Si bien el Registro Civil participa de la recepción y registro de hechos vitales, es la Dirección de Estadísticas e Información de Salud (DEIS) quien ofrece las cifras definitivas de defunciones y nacimientos, por los respectivos lugares de residencia de las personas a las que se refiere. En este trabajo, no obstante, se utilizó la información de las estadísticas vitales de la Ciudad de Buenos Aires, por lo que no se incluyen las defunciones ocurridas en otras jurisdicciones del país, correspondientes a personas fallecidas que tenían su residencia habitual en la Ciudad. Esto es porque –para la predicción estadística– en un contexto de confinamiento, como fue el año 2020 y gran parte del 2021, lo más probable es que la jurisdicción de residencia y la de fallecimiento coincidan, para el caso de la Ciudad de Buenos Aires.
Puntualmente, el registro de las defunciones se realiza sobre la base del certificado médico de defunción, que constata la muerte, y sobre la base del Informe Estadístico de Defunción, que informa sobre otras características de la persona fallecida, circunstancias y, principalmente, la causa o causas de muerte. Este informe es completado por el médico que certifica la muerte y, eventualmente, por la morgue judicial o el cuerpo forense en aquellos casos en los que la muerte es violenta y requiere su intervención. Estos informes, en Ciudad de Buenos Aires, son recolectados y digitalizados por la Dirección General de Estadística y Censos, que es la representante jurisdiccional de la Ciudad en el ámbito del Sistema Estadístico Nacional.
Un tema ineludible para el estudio de la mortalidad a partir de la información producida por los sistemas de estadísticas vitales y de registro civil es la calidad de los datos. Antes de la etapa de análisis, es necesario detectar los posibles errores que puedan afectar los datos. En la actualidad, se reconoce que los problemas de calidad son de naturaleza multivariada y pueden estar presentes en todas las etapas: diseño, recolección, procesamiento, elaboración, análisis o difusión de la información. Básicamente, son dos los tipos principales de errores: cobertura y contenido. El primero refiere a problemas en la enumeración de las muertes y deriva en contar de menos o de más la cantidad defunciones. El segundo tipo tiene que ver con errores en el completamiento de los Informes Estadísticos de Defunción.
En el marco de este trabajo, se utiliza el conteo de muertes por lo que el error que preocupa es el de cobertura y no el de contenido. La bibliografía de referencia reconoce factores que podrían contribuir con este error. Entre ellos, los más importantes son los siguientes (Naciones Unidas, 2014):
-
La inaccesibilidad de la población a la registración de los hechos por cuestiones geográficas, socioeconómicas o culturales. Este impedimento se profundiza especialmente cuando un número importante de las muertes acaecen fuera de las instituciones de salud.
-
La falta de delegaciones administrativas del registro civil.
-
La falta de articulación y el funcionamiento ineficiente del registro civil y el sistema de estadísticas vitales, especialmente en territorios grandes.
Particularmente, la Ciudad de Buenos Aires tiene bajo nivel de errores de cobertura. Primero porque dentro de la Argentina es la única jurisdicción 100% urbana, por lo que “todo queda cerca” y el registro de hechos vitales se completa. Pero, además, porque aquí en el país es indispensable certificar la muerte para acceder al permiso de cremación y entierro, por lo que el completamiento del Informe Estadístico de Defunción resulta un requisito ineludible. La Ciudad sí presenta, en cambio, incompletitud o imprecisiones en la información, aunque no afectan al presente estudio (Carpinetti et al., 2019; Ribotta, 2013; Ribotta, 2014; Ribotta 2016).
No puede pasarse por alto qué defunciones son contabilizadas cuando se hace referencia a una jurisdicción determinada y a un año determinado. En forma más directa, ¿a qué nos referimos cuando hablamos, por ejemplo, de las defunciones en la Ciudad de Buenos Aires del año 2016? Con respecto a la división territorial, aquí se la entiende como la jurisdicción donde residía habitualmente la persona y donde, además, se registró la muerte. La jurisdicción de ocurrencia de la muerte es, además, la de registro. Esto quiere decir que, si una muerte ocurrió en la Ciudad de Buenos Aires, se registra allí. Puede ocurrir, naturalmente, que la muerte suceda en la Ciudad de Buenos Aires, se registre allí, pero la persona fallecida tuviera su residencia habitual en la provincia de Chubut. En este caso, estas defunciones quedan excluidas de este trabajo. Se contabilizan, entonces, aquellas muertes ocurridas y registradas en la Ciudad de Buenos Aires, correspondientes a personas que residían en la Ciudad de Buenos Aires al momento del fallecimiento. Con respecto al año, es aquel en que se registró la muerte que, usualmente, no difiere del año en que ocurrió la muerte, puesto que en general la muerte se registra antes de que pasen tres días del fallecimiento y, en la mayoría de los casos, el registro se lleva adelante el mismo día en que se certifica la muerte.
Ante la existencia de defunciones ocurridas dos o más años antes del año de registro, que representan alrededor del 1,0 por mil del total de defunciones, se tomó la decisión de excluirlas, siguiendo los lineamientos del Ministerio de Salud de la Nación para el Sistema Estadístico de Salud.
Consideraciones conceptuales y metodológicas
En el contexto de este artículo, y siguiendo el documento base de la Organización Mundial de la Salud (World Health Organization, 2023), en adelante directamente “documento base”, se denomina “diferencia de mortalidad” al número de muertes de cualquier causa que sobrepasa o que resulta inferior al número de muertes que se hubiera esperado en “condiciones habituales”. Cuando esta diferencia es positiva, existe un “exceso de mortalidad” mientras que, análogamente, cuando esta diferencia es negativa hablamos de un “defecto de mortalidad”. Sobre estas ideas se trabaja, tanto en el documento base como aquí, prescindiendo de la población expuesta a riesgo y del cálculo de tasas. Las razones por las que se excluye la población expuesta se resumen en los siguientes puntos:
-
La incorporación de información acerca de la población incorpora otras fuentes de datos que adolecen de problemas que las estadísticas vitales no tienen: los problemas de cobertura.
-
Existe suficiente evidencia (Dirección General de Estadística y Censos, 2023) que da cuenta de que la población residente en la Ciudad de Buenos Aires se mantiene, desde 1950, en 3 millones de habitantes, sin sufrir cambios significativos. En tal sentido, los volúmenes de defunciones siempre refieren al mismo efectivo de población en términos aproximados, por lo que diferencias en las tasas de mortalidad son resultado directo de diferencias en las cantidades de defunciones. Las diferencias en la composición de la población por edad y sexo no son relevantes para este trabajo, puesto que el documento base sugiere utilizar el total de defunciones para preservar la comparabilidad y porque el breve período de estudio no presenta variaciones significativas en la estructura por sexo y por edad de la población (Dirección General de Estadística y Censos, 2016; Dirección General de Estadística y Censos, 2021).
Como se indicó, se procesaron las muertes ocurridas y registradas en la Ciudad de Buenos Aires, correspondientes a residentes de la Ciudad, por mes de registro. El conteo se hizo, por un lado, para las muertes infantiles (menores de un año de edad) y, por otro lado, para el resto de las defunciones (de 1 año de edad y más). Sin embargo, en este trabajo se presenta la información ya sumada, de forma tal que el número de muertes es el total.
Con la información de las muertes contabilizadas mes por mes hasta 2019, se procedió, como se indicó anteriormente, a realizar diferentes estimaciones para proyectar las muertes esperadas para cada mes de los años calendario 2020 y 2021, bajo el escenario supuesto sin pandemia; es decir, asumiendo que la tendencia observada se replicaría. Esto se hizo principalmente con cinco técnicas: suavización exponencial, Holt-Winters, SARIMA; Modelo binomial negativo con splines cúbicos cíclicos y redes neuronales LSTM. Los cinco métodos se describen directamente en la sección de resultados.
Mortalidad observada previa a 2020
Varios son los autores que describen la mortalidad del último tiempo en la Ciudad de Buenos Aires (Carpinetti y Lascano, 2022; Mazzeo, 2021). El propósito de esta sección no es caracterizar la mortalidad, sino presentar las cifras que serán insumo para las metodologías de estimación. En tal sentido, el Cuadro 1 presenta los resultados de la desagregación mensual de las muertes en la Ciudad, para los años calendario que sirven de insumo a las estimaciones objetivo de este trabajo.
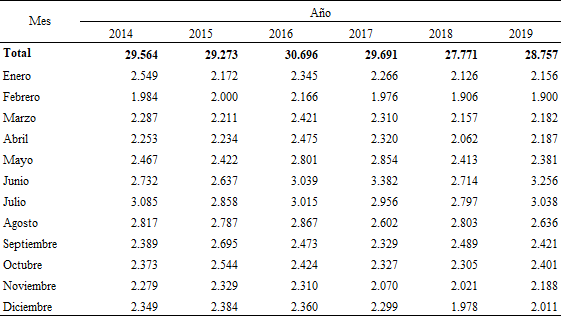
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
Se observa que, en términos generales, el número de defunciones de la Ciudad se mantiene alrededor de 29.000, habiendo alcanzado su máximo en el año 2016 y con una tendencia a la baja en los dos últimos años previos a la pandemia. Bajo la hipótesis nula de que las defunciones mensuales siguen una distribución normal con media y desvío igual a los observados en cada año, se calcularon los desvíos individuales estandarizados Zi y se observa que todos están razonablemente dentro de los límites de confianza de una normal estándar. Para facilitar la lectura se han marcado los desvíos estandarizados más altos en valor absoluto (Cuadro 2).
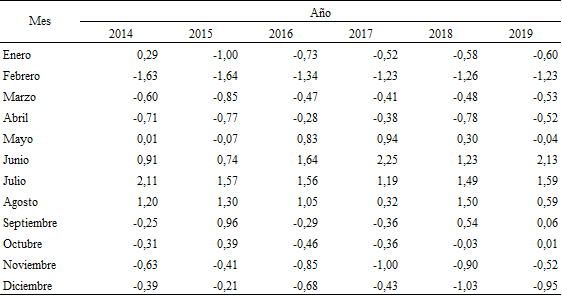
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
Si se observa nuevamente el Cuadro 1, hacia el interior de cada año, la distribución por mes no es uniforme. Como es de esperar, el mayor caudal de muertes se concentra en los meses de invierno. Para detectar si la distribución porcentual de muertes, a lo largo de un año, es constante año a año, se somete a prueba la hipótesis de homogeneidad (Chao, 1993). Bajo la hipótesis nula de que existe homogeneidad y que esta distribución porcentual se corresponde con aquella implícita en la distribución de muertes de todo el período 2014-2019, naturalmente, se obtiene un estadístico chi cuadrado de alto valor, producto de que los cuadrados de las diferencias entre las frecuencias observadas y las esperadas son altas, por la naturaleza misma de los datos.
Para ilustrar esta idea, nótese que durante todo el período 2014-2019 se observaron 175.752 defunciones, de las cuales 13.614 ocurrieron en los meses de enero. Esto implica que, aproximadamente, un 7,75% de las muertes ocurren, bajo hipótesis nula verdadera, en enero. Se esperaría entonces que, en 2014, de las 29.564 defunciones observadas para el total del año, un 7,75% ocurran en enero; es decir, aproximadamente 2.290. Lo observado, en cambio, para enero de 2014 fue 2.549 defunciones.
La contribución chi cuadrado hace referencia al cálculo aritmético del cociente entre el cuadrado de la diferencia entre las defunciones esperadas (2.290) y las observadas (2.549), y las defunciones esperadas (2.290). Para este ejemplo, tal número resulta ser 29,3. En el Cuadro 3 se presentan las contribuciones chi cuadrado, redondeadas al entero más próximo. Además, están sombreadas aquellas contribuciones elevadas que presentan información acerca de aquellos meses en los que lo observado es significativamente diferente de lo esperado bajo la hipótesis de homogeneidad.
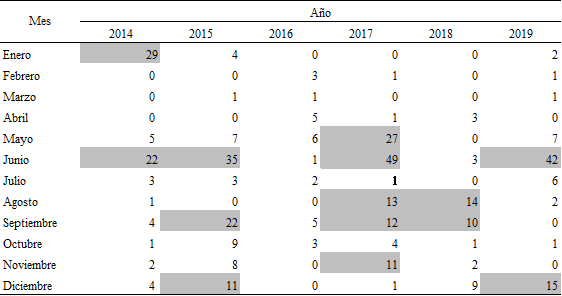
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
Como se ve, el mes de junio y, en general, el invierno representan el período que escapa al patrón. Incluso 2017 lo hace, pero interiorizarse en estas diferencias desviaría el objetivo del presente trabajo.
Estimación de la mortalidad para 2020 y 2021
La estimación del exceso (o defecto) de la mortalidad se puede realizar por año calendario completo. No obstante, habiendo visto que las defunciones en la Ciudad presentan alguna regularidad, pero que existe cierta estacionalidad, se procede a proyectar por separado las defunciones de cada mes de 2020 y de 2021. Esto se hizo con las diferentes propuestas metodológicas ya detalladas anteriormente:
- 1. Suavización exponencial
- 2. Holt-Winters
- 3. SARIMA
- 4. Modelo binomial negativo con splines cúbicos cíclicos
- 5. Redes neuronales LSTM
La primera propuesta metodológica consiste en considerar la serie de tiempo dada por las seis observaciones de enero (2014, 2015, 2016, 2017, 2018 y 2019) y, a partir de esas seis observaciones, estimar la séptima y la octava observación (2020, 2021) aplicando la técnica de suavización exponencial simple (análogamente se hace con los otros once meses del año). Por medio de esta técnica, se le confiere mayor ponderación a la información más reciente y, de la misma manera, las observaciones más distantes en el tiempo pierden gradualmente peso para la estimación. Se ha optado por la variación de Brown y Meyer dentro de esta técnica (Brown y Meyer, 1961).
Holt (1957) y Winters (1960) desarrollaron un método de suavizamiento exponencial triple que permite modelar la estacionalidad de una serie y que, como se indicó, es la segunda propuesta metodológica. Este método consiste en una ecuación de predicción y tres ecuaciones de suavizado: una para el nivel, otra para la tendencia y otra para el componente estacional, cada una con su parámetro de suavizado correspondiente. Ha de elegirse, para el modelo, una frecuencia del componente estacional, que aquí se optó porque fuera mensual. Así, cada mes se proyecta independientemente.
Para la tercera propuesta metodológica se plantea un modelo ARIMA estacional; es decir, un modelo SARIMA (Hyndman y Athanasopoulos, 2021). Este tipo de modelos se construye incluyendo términos estacionales adicionales al modelo ARIMA convencional. Al diferenciar la serie cada 12 meses, se obtiene el siguiente gráfico (Gráfico 1) y sus correspondientes correlogramas.
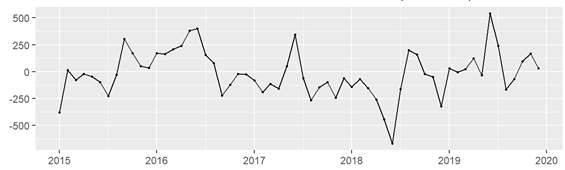
Gráfico 1
Diferencia primera de las defunciones mensuales. Ciudad de Buenos Aires. Enero 2015/diciembre 2019
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
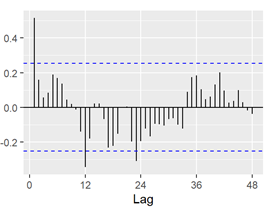
Gráfico 2
Función de autocorrelación parcial de las defunciones. Ciudad de Buenos Aires. Años 2014/2019
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
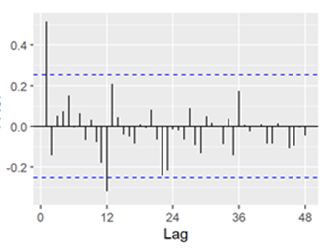
Gráfico 3
Función de autocorrelación de las defunciones. Ciudad de Buenos Aires. Años 2014/2019
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
Se puede observar (Gráfico 2 y Gráfico 3) que la función de autocorrelación parcial y la función de autocorrelación presentan un “pico” en el mes 12, lo que sugiere un proceso de medias móviles de orden 1; es decir, un proceso MA(1) estacional. Por otro lado, los picos en el mes 1 en ambos gráficos sugieren también un proceso autorregresivo de orden 1; es decir, un AR(1) no estacional. Coincidentemente, este es también es el modelo que arroja la función auto.arima del paquete forecast de R (R Core Team, 2020).
El coeficiente AR(1) estimado es 0,538 con un error estándar de 0,112, y el MA(1) estacional estimado es -0,5588 con un error estándar de 0,1498. Los residuos resultantes del modelo se han graficado para evaluar su correlación serial y la posibilidad de que tengan distribución normal (Gráfico 4 y Gráfico 5).
Se ha efectuado la prueba Ljung-Box de los residuos, la cual arroja un valor p de 0,9795, por lo que no se rechaza la hipótesis nula de que los residuos no están serialmente correlacionados. Cumplidos los supuestos necesarios para la aplicación del modelo SARIMA, se han estimado las defunciones siguiendo el procedimiento habitual con los coeficientes indicados anteriormente.
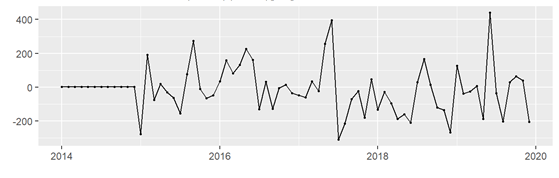
Gráfico 4
Residuos del modelo ARIMA. Ciudad de Buenos Aires. Años 2014/2019
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
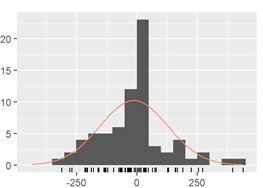
Gráfico 5
Histograma de residuos del modelo ARIMA. Ciudad de Buenos Aires. Años 2014/2019
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
La cuarta metodología sigue el procedimiento principal planteado y defendido en el documento base para los países con información histórica mensual. Aquí se plantea que la cantidad de defunciones mensuales es una variable aleatoria que se distribuye como una binomial negativa, en la cual el logaritmo natural de la esperanza matemática se modela con una forma funcional lineal. Para capturar la estacionalidad se utilizan splines cúbicos cíclicos (World Health Organization, 2023).
La quinta propuesta metodológica es la de redes neuronales LSTM (Long Short-Term Memory). Se trata de un tipo de red neuronal recurrente que surgió como una solución a los problemas de desvanecimiento del gradiente o gradiente explosivo (Hochreiter y Schmidhuber, 1997). Las redes neuronales recurrentes son una extensión de las redes neuronales clásicas, en tanto permiten que el insumo sea una secuencia. Presentan como desventaja el llamado desvanecimiento del gradiente, que ocurre cuando la información del insumo o del gradiente pasa a través de varias capas de la red, y termina desvaneciéndose al llegar al final o al comienzo de la red neuronal. No obstante, su propiedad secuencial las hace útil al presente trabajo. La arquitectura de la red consta de una primera capa LSTM de 100 unidades, seguida de una capa Dense de 50 unidades, y una última capa Dense de 12 unidades. La función de pérdida es el error cuadrático medio y se implementó el algoritmo Adam para la optimización. Se programó en Python con la librería TensorFlow y se utilizaron ventanas deslizantes para aprovechar al máximo la serie temporal al entrenar la red neuronal.
A continuación, se presentan las estimaciones de las defunciones mensuales para la Ciudad de Buenos Aires para 2020 (Cuadro 4) y para 2021 (Cuadro 5); es decir, aquellas proyectadas bajo un escenario sin pandemia y para las cinco propuestas metodológicas.
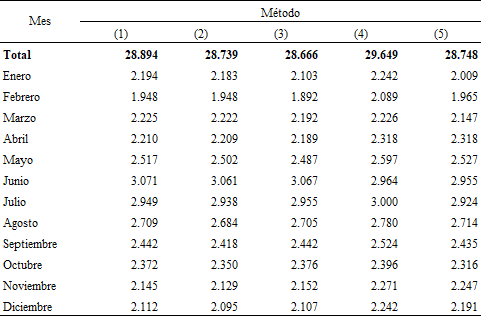
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.1 los modelos de estimación son (1) Suavizamiento exponencial, (2) Holt-Winters, (3) SARIMA, (4) Binomial negativo y (5) Redes neuronales LSTM.
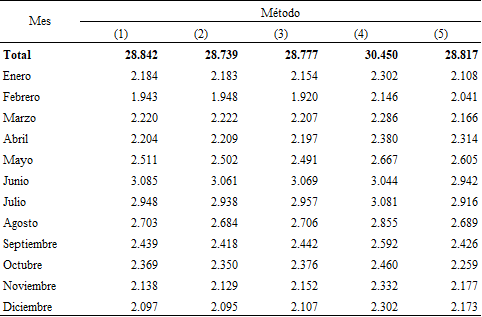
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.1 los modelos de estimación son (1) Suavizamiento exponencial, (2) Holt-Winters, (3) SARIMA, (4) Binomial negativo y (5) Redes neuronales LSTM.
A los efectos de tener una impresión gráfica, se ha optado por presentar los resultados de los cuadros anteriores en un gráfico de líneas (Gráfico 6). Conscientes de que este tipo de gráfica es idónea para variables continuas de observación continua y no para este caso, resulta mejor –en virtud de la cantidad de datos– que presentar diagramas de barras. Incluso permite apreciar la estacionalidad del fenómeno y la poca diferencia entre todas las estimaciones.
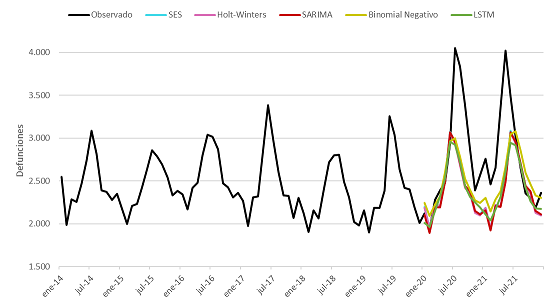
Gráfico 6
Defunciones mensuales observadas y estimadas. Ciudad de Buenos Aires. Enero 2014/diciembre 2021
Fuente: elaboración propia sobre Cuadro 1, Cuadro 4 y Cuadro 5.
Como se observa, todas las propuestas metodológicas arrojan valores similares excepto la cuarta propuesta: el modelo binomial negativo. Este modelo pareciera sobreestimar las muertes mensuales. En 21 de los 24 meses que comprenden 2020 y 2021, predice muertes por encima de los otros cuatros métodos, por lo que será descartado para el análisis del exceso de mortalidad. Como se indicó anteriormente, el modelo (binomial negativo) es un método en esencia econométrico. Algunos estudios sugieren que adolece del conocido problema de “sobredispersión” en los datos de conteo, que el modelo supone constante a lo largo del tiempo. Es posible que este supuesto no se esté cumpliendo y que deba recurrirse a otros modelos (Luque-Fernandez et al., 2016; Mutiso et al., 2021). En virtud de las estimaciones tan diferentes con respecto a los otros, este modelo no será tenido en cuenta para el análisis de estos resultados.
Análisis de resultados
En lugar de elegirse un método de estimación entre los cuatro que se han considerado aceptables, se optó por un escenario pesimista: en cada mes de 2020 y 2021, se supone que las muertes esperadas son las indicadas por la propuesta metodológica que, para ese mes, haya arrojado mayor valor. De esa manera, si se hubieran observado en la Ciudad aún más defunciones que las estimadas, se atribuirían a todo el proceso de pandemia.
A continuación, se presenta la estimación para este escenario pesimista y se lo contrasta con las muertes observadas y registradas por el sistema de estadísticas vitales de la Ciudad (Cuadros 6 y 7). Se ha optado por sombrear las cifras que se presentan en los meses donde se observó menor mortalidad que la esperada.
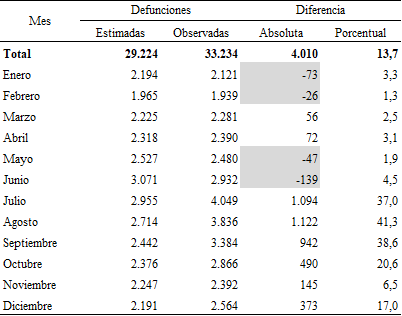
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
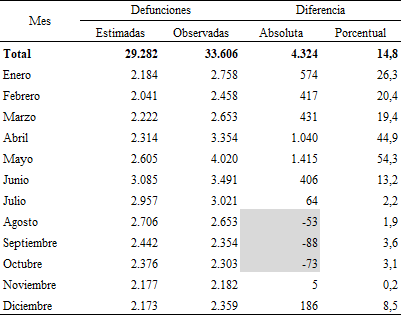
Fuente: elaboración propia sobre la base de Dirección General de Estadística y Censos (Ministerio de Hacienda y Finanzas. GCBA). Estadísticas vitales.
Se observa que, salvo casos aislados, las diferencias por mortalidad son excesos de mortalidad; es decir, la incidencia del virus, junto con la pandemia, habrían contribuido para experimentar mayor nivel de mortalidad que el esperado. Esta conclusión se ha observado en varios países: en efecto, existe sólida evidencia que da cuenta de que el balance entre vidas perdidas y vidas ganadas por el fenómeno de la pandemia y la cuarentena termina eventualmente resultando con saldo negativo (Hale et al., 2020; Knutson et al., 2023; Msemburi et al., 2023; Rivera et al., 2020). Ha de notarse que, en enero y en febrero de 2020, hay un defecto de mortalidad, lo que vendría dado porque, evidentemente, la mortalidad venía en disminución y el confinamiento empezó recién en marzo de ese año. El invierno de 2020, resultó ser, como era de esperarse, el bimestre más golpeado: aún no existía vacuna y el virus alcanzaba su letalidad máxima. Tal como se indica en el Cuadro 6, se esperaban en el año 29.224 defunciones y se observaron 33.234 defunciones; es decir, casi un 14% más. Ese porcentaje, sin embargo, esconde las heterogeneidades resultantes de la propia estacionalidad del efecto mortalidad y de la novedad del escenario mundial. Como puede apreciarse, en los meses de julio, agosto y septiembre de ese año, las diferencias respecto de lo esperado, aun tomando el escenario más pesimista, superan el 35%.
En el año 2021, en cambio, si bien el número total de defunciones observadas superó en un 15% al esperado, y esto resulta similar a la experiencia del año anterior, la sorpresa se presenta en los meses de abril y mayo, puesto que presentaron mayor exceso de mortalidad. Esto podría presuntamente deberse a la aparición concomitante de las variantes Alpha, Gamma y Andina en nuestro país (Proyecto Argentino Interinstitucional de Genómica de SARS-Cov-2, 2021). En general, durante todo el año se observaron más muertes que las esperadas, excepto en los meses de agosto, septiembre y octubre, aquí posiblemente por la efectividad de las vacunas, aunque las diferencias son igualmente pequeñas.
El siguiente gráfico (Gráfico 7) permite apreciar las diferencias porcentuales de mortalidad experimentadas durante los dos años.
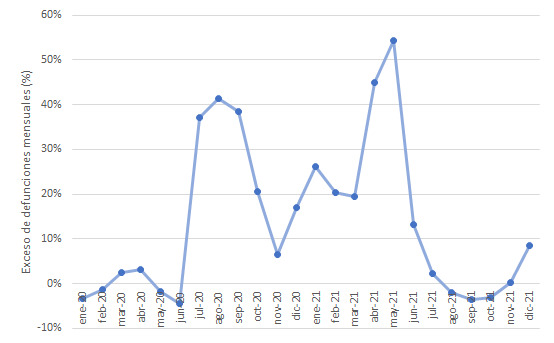
Gráfico 7
Excesos y defectos porcentuales de mortalidad. Ciudad de Buenos Aires. Enero 2020/diciembre 2021
Fuente: elaboración propia sobre Cuadro 6 y Cuadro 7.
El análisis de los datos en términos de “olas” de la pandemia exige, naturalmente, delimitar estas olas, lo cual lleva a una discusión teórica que no admite un consenso único. Algunos autores (Burton et al., 2023; Irassar et al., 2022) coinciden –aunque no están estrictamente de acuerdo en las fechas puntuales– en reconocer tres en Argentina: la primera ola prácticamente abarca desde marzo a noviembre de 2020 con un pico máximo en agosto. La segunda ola, un rebrote en verano de 2021. Y la tercera ola, caracterizada por nuevas cepas, durante abril y mayo de 2021. Cabe aclarar que existiría una cuarta ola, pero ya en el año 2022, que este trabajo excluye.
Conclusión
La pandemia COVID-19 trajo consigo un aumento de muertes por la aparición de una nueva causa, pero la situación de confinamiento y de pandemia, a su vez, pudo haber venido acompañada por una reducción en muertes por otras causas. En este artículo, se buscó responder a la pregunta de investigación sobre si el saldo resultante entre defunciones no esperadas y defunciones evitadas realmente provocó una diferencia en el comportamiento esperado del nivel de mortalidad en la Ciudad De Buenos Aires. Para ello, ha sido necesario cuantificar la diferencia de mortalidad generada por estos cambios, para lo cual se siguieron las recomendaciones de Naciones Unidas. Se observó, casi sin excepción, que todo el paquete pandémico produjo un exceso de muertes, revirtiendo la tendencia de la mortalidad en descenso.
Independientemente del método con el que se pronostiquen las muertes esperadas por todas las causas, la tendencia general muestra que la Ciudad de Buenos Aires tuvo cerca de un 15% de muertes adicionales por la aparición del COVID-19 y todos los efectos que de allí se desprenden. Sin embargo, esta variación no es uniforme dentro del año y, por el contrario, presenta marcadas diferencias. Mientras que en el año 2020 las diferencias más notorias se ubican en los meses de invierno, en el año 2021 ocurren antes: durante abril y mayo, para luego disminuir incluso a niveles mucho menores. Debe atenderse, sin embargo, al hecho de que una de las cinco propuestas metodológicas expuestas en el trabajo ha arrojado diferencias sustanciales respecto de las otras cuatro, por lo que incorporarla en las conclusiones produciría distorsiones. No obstante, y prosiguiendo con el objetivo de este trabajo que es presentar los resultados de estimaciones surgidas de procedimientos econométricos, es que los mismos se han presentado, pero se ha evitado su interpretación.
Resultaría de interés extender este análisis a todo el país, desagregado por provincia y, en la medida que los datos lo permitan y que la calidad no se vea afectada, reproducir el trabajo separando las muertes por sexo o por grupos de edad, puesto que se sabe que la mortalidad es diferencial por sexo y por edad y, en este trabajo, puede haber efectos contrarios que coadyuven a explicar resultados que, a primera vista, puedan precisar un análisis más pormenorizado.
Bibliografía
Brown, R. y Meyer, R. (1961) The Fundamental Theorem of Exponential Smoothing. Operations Research,9(5), 673-685. https://doi.org/10.1287/opre.9.5.673
Burton, B., Lugones, M., Barrios García Moar, G., Murriello, S. y Bengtsson, A. (2023). La pandemia por COVID-19 en Argentina. Universidad de Costa Rica. http://rid.unrn.edu.ar/handle/20.500.12049/10255
Carpinetti, E., Lascano, V., Dayan, F. y Dimaro, L. (2019). Informe Técnico: Estadísticas vitales en la Ciudad de Buenos Aires. Población de Buenos Aires, 16(28), 34-49. https://revista.estadisticaciudad.gob.ar/ojs/index.php/poblacionba/issue/view/4/8
Carpinetti, E. y Lascano, V. (2022). La mortalidad en la Ciudad de Buenos Aires en las últimas tres décadas. Población de Buenos Aires, 19(31), 28-69. https://revista.estadisticaciudad.gob.ar/ojs/index.php/poblacionba/issue/view/1/6
Cavaillon, J. & Osuchowski, M. (2021). COVID-19 and earlier pandemics, sepsis, and vaccines: A historical perspective. Journal of Intensive Medicine, 1(01), 4-13. https://doi.org/10.1016/j.jointm.2021.04.003
Chao, L. (1993). Estadística para las ciencias administrativas. McGraw-Hill.
Dirección General de Estadística y Censos (2016). Encuesta Anual de Hogares 2015. Estructura de la población. Informe de Resultados 1025. Ministerio de Hacienda y Finanzas. Ciudad de Buenos Aires. https://www.estadisticaciudad.gob.ar/eyc/wp-content/uploads/2016/07/ir_2016_1025.pdf
Dirección General de Estadística y Censos (2021). Encuesta Anual de Hogares 2020. Estructura de la población. Informe de Resultados 1604. Ministerio de Hacienda y Finanzas. Ciudad de Buenos Aires. https://www.estadisticaciudad.gob.ar/eyc/wp-content/uploads/2021/11/ir_2021_1604.pdf
Dirección General de Estadística y Censos (2023). Crecimiento y estructura de la población. En Dirección General de Estadística y Censos. Anuario Estadístico 2022. (pp. 25-32). Ministerio de Hacienda y Finanzas. Ciudad de Buenos Aires. https://www.estadisticaciudad.gob.ar/eyc/wp-content/uploads/2023/06/Anuario_estadistico_2022_web.pdf
Djakaria, I. y Saleh, S. (2021). Covid-19 forecast using Holt-Winters exponential smoothing. Journal of Physics: Conference Series 1882(1), 012033. DOI 10.1088/1742-6596/1882/1/012033
Guleryuz, D. (2021). Forecasting outbreak of COVID-19 in Turkey; Comparison of Box–Jenkins, Brown’s exponential smoothing and long short-term memory models. Process Safety and Environmental Protection, 149, 927-935. https://doi.org/10.1016/j.psep.2021.03.032
Hale, T., Angrist, N., Kira, B., Petherick, A., Phillips, T. y Webster, S. (2020). Variation in government responses to COVID-19. Technical report, University of Oxford.
Hochreiter, S. y Schmidhuber, J. (1997). Long short-term memory. Neural Computation, 9(8), 1735-1780.
Holt, C. C. (1957). Forecasting seasonals and trends by exponentially weighted averages. International Journal of Forecasting, 20(1), 1-5. https://doi.org/10.1016/j.ijforecast.2003.09.015
Hyndman, R.J. y Athanasopoulos, G. (2021) Forecasting: principles and practice. OTexts.
Irassar, J., Bartel, E., Obando, D., & Varela, T. (2022). Comparación epidemiológica de las olas por COVID-19 en la provincia de Buenos Aires, Argentina, 2020-2021. Revista Argentina de Salud Pública, 14, 49-49.
Jain, A., Sukhdeve, T., Gadia, H., Sahu, S. P., & Verma, S. (2021). Covid19 prediction using time series analysis. 2021 International conference on artificial intelligence and smart systems (ICAIS) (pp. 1599-1606). https://doi.org/10.1109/ICAIS50930.2021.9395877
Karlinsky, A. (2022). Estimating national excess mortality from subnational data: application to Argentina. Revista Panamericana de Salud Pública, 46. https://doi.org/10.26633/RPSP.2022.19
Knutson, V., Aleshin-Guendel, S., Karlinsky, A., Msemburi, W. y Wakefield, J. (2023). Estimating global and country-specific excess mortality during the COVID-19 pandemic. Annals of Applied Statistics,17(2), 1353-1374. https://doi.org/10.1214/22-AOAS1673
Lachenal, G. y Thomas, G. (2020). COVID-19: When history has no lessons. History Workshop, 30.
Luque-Fernandez, M., Belot, A., Quaresma, M., Maringe, C., Coleman, M. y Rachet, B. (2016). Adjusting for overdispersion in piecewise exponential regression models to estimate excess mortality rate in population-based research. BMC medical research methodology, 16(1), 1-8. https://doi.org/10.1186/s12874-016-0234-z
Mazzeo, V. (2021). La mortalidad entre siglos por enfermedades respiratorias en la Ciudad de Buenos Aires ¿Las muertes por pandemias del siglo XXI las superaron? Población de Buenos Aires, 18(30), 5-20. https://revista.estadisticaciudad.gob.ar/ojs/index.php/poblacionba/article/view/1
Ministerio de Salud de Nación (2022). Información Básica. Buenos Aires, Dirección Estadística e Información de Salud. Años 2014 a 2019. Serie 5 N° 58 a 65. https://www.argentina.gob.ar/salud/deis/publicaciones
Msemburi, W., Karlinsky, A., Knutson, V. Aleshin-Guendel, S., Chatterji, S. y Wakefield, J. (2023). The WHO estimates of excess mortality associated with the COVID-19 pandemic. Nature 613, 130-137. https://doi.org/10.1038/s41586-022-05522-2
Mutiso, F., Pearce, J., Benjamin-Neelon, S., Mueller, N., Li, H, y Neelon, B. (2022). Bayesian negative binomial regression with spatially varying dispersion: Modeling COVID-19 incidence in Georgia. Spatial Statistics, 100703. https://doi.org/10.1016/j.spasta.2022.100703
Naciones Unidas (2003). Principios y recomendaciones para un sistema de estadísticas vitales. Revisión 2. Naciones Unidas.
Naciones Unidas (2014). Los datos demográficos. Alcances, limitaciones y métodos de evaluación. CEPAL, Serie Manuales N° 82.
Nikparvar, B., Rahman, M., Hatami, F. y Thill, J. C. (2021). Spatio-temporal prediction of the COVID-19 pandemic in US counties: modeling with a deep LSTM neural network. Scientific reports, 11(1), 21715. https://doi.org/10.1038/s41598-021-01119-3
Perone, G. (2022). Using the SARIMA model to forecast the fourth global wave of cumulative deaths from COVID-19: Evidence from 12 hard-hit big countries. Econometrics, 10(2), 18. https://doi.org/10.3390/econometrics10020018
Pitlik, S. (2020). COVID-19 compared to other pandemic diseases. Rambam Maimonides medical journal, 11(3).
Proyecto Argentino Interinstitucional de Genómica de SARS-Cov-2 (2021). Reporte N°23: Vigilancia de variantes de SARS-CoV-2 en la CABA, provincias de Buenos Aires, Córdoba, Entre Ríos, Neuquén y Santa Fe. Actualización del 07/06/2021.
R Core Team (2020). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Ribotta, B. (2013, 18-20 de septiembre). Precisión de los datos sobre defunciones del Sub-Sistema de Estadísticas Vitales de la Argentina (2001-2009) [Presentación en jornadas]. XII Jornadas Argentinas de Estudios de Población. Bahía Blanca, Argentina.
Ribotta, B. (2014). Evaluación de la exactitud de los datos sobre la causa básica de muerte en América Latina. Revista Peruana de Epidemiología, 18(3), 1-9. http://hdl.handle.net/11336/39429
Ribotta, B. (2016). Causas de defunción mal definidas en las provincias de Argentina, 2001-2013. Memorias del Instituto de Investigaciones en Ciencias de la Salud, 14(3), 86-95. https://doi.org/10.18004/mem.iics/1812-9528/2016.014(03)86-095
Rivera, R., Rosenbaum, J. y Quispe, W. (2020). Excess mortality in the United States during the first three months of the COVID-19 pandemic. Epidemiology and Infection, 148. https://doi.org/10.1017/S0950268820002617
Safi, S. y Sanusi, O. (2021). A hybrid of artificial neural network, exponential smoothing, and ARIMA models for COVID-19 time series forecasting. Model Assisted Statistics and Applications, 16(1), 25-35. https://doi.org/10.3233/MAS-210512
Winters, P. R. (1960). Forecasting sales by exponentially weighted moving averages. Management Science, 6(3), 324-342. https://doi.org/10.1287/mnsc.6.3.324
World Health Organization (2023). Methods for estimating the excess mortality associated with the COVID-19 pandemic.